

- "Ориентир 3, вправо 10, больше 2, пулемет под желтым кустом ведет огонь по нашей пехоте", - четко передал телефонист командиру орудия.
Несколько секунд - и командир разыскал указанный ему пулемет. Правда, он был еле виден даже в бинокль - до него было 2 километра, - но огонь этого пулемета мог нанести пехоте большие потери: надо было во что бы то ни стало и как можно скорее заставить его замолчать. Трудная, но почетная для артиллериста задача.
Уверенно подал командир необходимые команды. Он знал свою полковую пушку и свой орудийный расчет, состоявший из бойцов-отличников. У него все было тщательно подготовлено и рассчитано. Он не даром 2 года учил своих бойцов работать при орудии быстро и точно.
Вот прозвучал первый выстрел. Разрыв не надо было искать - темный фонтан земли и дыма взметнулся перед кустом. Казалось, что снаряд уничтожил и куст, и спрятавшийся за ним пулемет.
Но пулемет продолжал стрелять.
Второй снаряд разорвался чуть позади куста.
Третий выстрел - и куст вместе с пулеметом исчезли с поля боя. На этот раз снаряд точно попал в цель.
Пулемет умолк. Наша пехота могла двигаться вперед. Задача была решена артиллеристами быстро и точно.
Все это было на учебной стрельбе. "Пулемет" и "пулеметчики" противника были сделаны из обыкновенных досок.
Когда стрельба окончилась и бойцы осматривали мишени, они действительно убедились в уничтожении "пулемета". Снаряд в щепки разбил и разбросал щит, обозначавший пулемет, и две мишени "пулеметчиков"; третья, пробитая десятком осколков, была похожа на решето.
Так было на учебном поле, но все понимали, что так будет и на поле боя, когда понадобится точная работа наших артиллеристов, призванных со всей Красной Армией защищать свою Родину.
Но почему назвали мы эту стрельбу точной?
Разве не могли артиллеристы попасть в цель первым снарядом?
Мы вскоре ответим на этот вопрос. Прежде же спросим себя: что значит слово "точно", какой смысл вкладываем мы в него?
Часто говорят, например: "Мои часы ходят точно". Что подразумевают в этой случае? Рассчитывают ли тут на абсолютно точное совпадение часов, положим, с астрономическим хронометром?
Конечно, нет. Несколько десятых или сотых секунды - какая-нибудь погрешность непременно имеется. Но мы знаем, что такая погрешность в житейском обиходе значения не имеет, и мы с ней миримся.
"Точно" в этом случае значит: с погрешностью, скажем, не более, чем одна секунда.
Другое дело, когда на пригласительном билете написано: "Начало точно в 19 часов". Тут уж никто не будет рассчитывать на точность до 1 секунды. В этом случае мы помиримся с погрешностью в несколько минут.
Проверяя купленную в магазине материю, мы, вероятно, запротестуем, если ошибка будет измеряться сантиметрами, но даже не заметим ошибки в несколько миллиметров.
Другое дело, если на те же несколько миллиметров будет допущена ошибка в диаметре канала ствола орудия. В этом случае мы не только не признаем работу точной, но забракуем ее, как явно негодную и грубую. Ошибку же на сотые доли миллиметра мы и тут сочтем нормальной, а орудие с такой ошибкой - вполне точным.
Таких примеров можно было бы привести сколько угодно. Всегда и всюду мы натыкаемся, в конце концов, либо на предел точности, когда мы вынуждены допускать некоторую погрешность, либо большая точность просто не нужна.
Теперь, когда мы выяснили условность понятия "точно", вернемся к нашему примеру. Какая точность стрельбы требовалась от артиллеристов, чтобы уничтожить пулемет?
Это рассчитать нетрудно. Щит, изображавший пулемет, имел размеры 1 x 1 метр. Снаряд мог попасть в середину щита, в любой его край, - все равно "пулемет" был бы уничтожен. Граната полковой пушки дает воронку радиусом около 75 сантиметров: попадание снаряда не далее 75 сантиметров от щита несомненно поразит "пулемет". Значит, погрешность в десяток сантиметров здесь, очевидно, не имеет никакого значения. Но на метры уже нельзя ошибиться. В этом случае пулемет может не получить "смертельного поражения".
Иными словами: отклонения снарядов от центра цели при данной стрельбе должны быть примерно менее одного метра.
Какова же должна быть при этом точность положения ствола орудия при выстреле?
Оказывается, при "идеальных" условиях, на которые рассчитаны "Таблицы стрельбы", снаряд должен вылететь из этого орудия под углом ровно в 81 "тысячную". Тогда он упадет ровно в 2000 метрах от орудия. Если же он вылетит под углом в 80 или 82 "тысячных", он уже не попадет в цель. Он упадет на 20 метров ближе или дальше цели. Расчеты показывают, что изменение угла бросания даже на 1/20 "тысячной" вызовет уже отклонение точки падения снаряда более чем на один метр.
Необходима, значит, точность до 1/20 "тысячной". А что значит на деле такая точность? Это значит: если дуло ствола сместится вверх или вниз от нужного положения на 0,05 миллиметра - на толщину тончайшего волоса, - снаряд полетит уже не по той траектории, которая нужна.
Отклонение траектории на толщину волоса в самой ее начале превратится в конце траектории - у цели - в отклонение на целые метры.
Конечно, наводчик, придавая нужный угол возвышения стволу, смотрит не на положение его дула, а на показания прицельных приспособлений орудия. Но эти приспособления имеют также свой предел точности, и этот предел много больше, чем 1/20 "тысячной".
Таким образом, самый искусный наводчик, в самом лучшем случае, не может гарантировать такой точности наводки, при которой на 2 километра все снаряды полковой пушки попадали бы в щит размерами 1x1 метр. Тут в дело вмешивается случайность -удача.
Однако удача может притти только к тому, кто обладает умением. Наводчик-новичок делает ошибки гораздо больше, чем в одну "тысячную", и ошибки эти допускает он то в одну, то в Другую сторону. При такой грубой работе в цель попасть, конечно, труднее: слишком велики пределы допускаемой погрешности.
Опытный, умелый наводчик тоже обычно допускает некоторую неточность, но уже самую маленькую, какую только позволяют прицельные приспособления. Такой наводчик, конечно, гораздо скорее попадет в ту же цель при всех тех же условиях.
Очевидно, что все сказанное об угле возвышения орудия касается и направления его в горизонтальной плоскости: если ствол направить чуть правее или левее цели, то снаряд также не попадет в цель.
Но все искусство любого наводчика пропало бы даром, если бы механизмы наводки были в плохом состоянии, если бы они были расстроены.
Механизмы наводки и прицельные приспособления надо всегда держать в чистоте. Загрязнение их способствует изнашиванию отдельных частей и образованию "мертвых ходов", влияющих на точность наводки. Мертвый ход - это ход впустую одной из частей механизма, которая должна передавать движение другой части этого же механизма.
Чтобы устранить вредное влияние мертвого хода какого-либо механизма, например подъемного механизма прицела, нужно назначенное деление прицела подводить к неподвижному указателю всегда снизу или всегда сверху. Сильно изношенные механизмы необходимо своевременно ремонтировать, чтобы мертвые хода не превзошли допустимых пределов.
При порче механизмов наводки орудие начинает как бы капризничать: оно посылает каждый снаряд по-иному. Тогда, конечно, нечего и думать о том, чтобы попасть в цель третьим снарядом: можно выпустить сотню снарядов и все же не попасть в цель.
Нам становится ясным, что орудие в нашем примере было в хорошем состоянии: о нем, очевидно, тщательно заботились, часто чистили его. Благодаря этому оно и не подвело наводчика, когда настал момент стрелять.
Все это касается наводки орудия, придачи орудийному стволу правильного вертикального и горизонтального углов.
Но дело не только в положении ствола, а еще и в скорости полета снаряда.
Прицел полкового орудия рассчитан на то, что его снаряд должен вылететь со скоростью 381 метр в секунду. Лишь в этом случае и при прочих "идеальных" условиях снаряд пролетит назначенное ему расстояние. Во всех остальных случаях он упадет дальше или ближе.
Установлено, например, что увеличение начальной скорости снаряда этой пушки всего на 1 метр в секунду вызовет уже отклонение снаряда от цели на 6 метров.
Но имеется очень много причин, которые могут уменьшить или увеличить начальную скорость на 1 метр в секунду и даже гораздо больше.
Начнем хотя бы с того, что чем больше выстрелов сделано из орудия, чем чаще они следовали один за другим, тем сильнее нагреется, а вместе с тем и расширится ствол. Таким образом, условия горения пороха для каждого выстрела будут изменяться (будет неодинаковый объем зарядной каморы); изменится и сила трения снарядов о стенки ствола. В результате, снаряды получат разные начальные скорости.
Затем, большое значение имеет правильное заряжание орудия. Если снаряды при заряжании не досылаются, то-есть вкладываются в ствол недостаточно глубоко, то при выстрелах создаются различные условия для сгорания пороха в зарядной каморе, а это вызывает разнообразие начальных скоростей снарядов. Заряжающий должен так вложить снаряд в орудие, чтобы почувствовать, что ведущий поясок снаряда подошел вплотную к началу нарезов.
Очень большое значение имеет при стрельбе и состояние канала ствола орудия.
Если на внутренней поверхности ствола имеются хотя бы самые ничтожные царапины, раковины или другие неровности (например, смяты или стерты поля нарезов), то при выстрелах может происходить прорыв газов, при каждом выстреле иной. При этом та или иная часть полезной энергии пороховых газов будет пропадать даром, и снаряды полетят с разными начальными скоростями.
Бороться с этим можно только заботой об исправном состоянии ствола. Надо всегда помнить, что орудие - сложная машина, она требует тщательного ухода и бережного отношения к себе.
И тут мы можем сказать: едва ли наши артиллеристы, стрелявшие по пулемету, получили бы такие хорошие результаты, если бы они не смазывали своевременно канал ствола, не протирали его аккуратно и насухо перед стрельбой, не вытирали тщательно снаряды и гильзы при заряжании.
Все эти "мелочи" необычайно важны. Ствол орудия не терпит ни грязи, ни песка, ни воды. Достаточно попасть в ствол нескольким песчинкам, чтобы при выстреле на поверхности канала получилась царапина. А каждая ничтожная царапина отзовется потом на скорости снаряда. Сырость в стволе вызовет появление ржавчины, а затем и раковин. Меткая стрельба станет почти невозможной.
На скорость снаряда оказывает также влияние качество пороха в заряде. К сожалению, добиться полной однородности пороха невозможно. Заряды не бывают абсолютно одинаковыми, даже если они изготовлены в одно время и на одном заводе. Каждый заряд содержит порох несколько иного качества. Сгорание пороха происходит то чуть быстрее, то чуть медленнее, и это опять-таки приводит к тому, что снаряды вылетают с разными скоростями.
Разнородность зарядов невелика и сравнительно мало отзывается на различии в начальной скорости полета снарядов. Но это различие резко возрастет, если патроны будут храниться небрежно. В состав пороха входят летучие вещества - спирт и эфир. Они легко испаряются, и при неправильном хранении может получиться так, что один заряд будет больше затронут испарением, другой- меньше. В результате появятся большие отклонения от нормальной начальной скорости снарядов.
Особые предосторожности принимают артиллеристы при подготовке зарядов к стрельбе: они выкладывают заряды в тени, прикрывают их ветками или брезентом, чтобы они не нагрелись и температура всех зарядов была одинакова. Иначе, при разной температуре зарядов, будут разные начальные скорости снарядов.
Разнобой в полете снарядов вызывается еще и тем, что самые снаряды не бывают в точности одинаковыми: снаряды, хотя и очень незначительно, но все же отличаются один от другого весом. Трудно, даже невозможно, изготовить снаряды в точности одного веса: хоть на грамм, хоть на долю его, но непременно один снаряд окажется тяжелее или легче другого. А при одинаковой силе заряда снаряд, имеющий меньший вес, вылетит из орудия с несколько большей скоростью, нежели снаряд, более тяжелый.
Эти различия, столь тонкие, что мы их даже не можем уловить нашими органами чувств, оказывают довольно большое влияние на полет снарядов. Если один снаряд весит, например, 6 500 граммов, а второй 6512, то при прочих равных условиях первый упадет на 1 метр дальше второго.
Уничтожить вполне это различие мы при нынешнем состоянии техники еще не имеем возможности. Но все же и здесь мы можем и обязаны сузить пределы погрешности.
Этого и добиваются артиллеристы при всякой к тому возможности. Они знают, что на снарядах всегда имеются отметки, указывающие на отклонение их веса от нормального (рис. 197). Вот по этим отметкам они и сортируют снаряды и стреляют подряд только одинаково отмеченными снарядами, например только с отметкой "Н" (нормальный вес) или только с отметкой "-" (несколько меньше нормального).
 |
| Рис. 197. Бойцы подготавливают снаряды к стрельбе: они сортируют их по весу |
Кроме того, и по форме - хотя это и незаметно на-глаз, - снаряды слегка отличаются друг от друга. Более шероховатый снаряд быстрее теряет скорость и ближе падает. Снаряды с разными очертаниями также испытывают различное сопротивление воздуха и падают в разных местах.
Наконец, на полете снарядов отзываются еще температура воздуха и ветер, его скорость и направление.
Предположим, первый выстрел пришелся на тот момент, когда облако прикрыло солнце и поднялся ветер, дующий навстречу снаряду. А перед вторым выстрелом солнце выглянуло из-за облака и ветер стих. Из-за этого второй снаряд залетит на несколько метров дальше, чем первый.
Тут, конечно, мы ничего не можем сделать: солнце и ветер не подчиняются нам.
Выводом из всего сказанного является одно: абсолютного единообразия условий стрельбы достичь невозможно.
Не существует и не может существовать такого орудия, которое бросало бы все свои снаряды в одну и ту же точку.
Как бы тщательно мы ни вели стрельбу, нацеливая орудие все время в одну и ту же точку, все равно снаряды упадут в разные места. Один упадет немного дальше, другой ближе, один правее, другой левее.
На рисунке 198 показаны траектории летящих снарядов, выпущенных из одного орудия в возможно одинаковых условиях. Все эти траектории образуют расходящийся сноп. Подобный сноп траекторий можно увидеть своими глазами, если стрелять так называемыми трассирующими снарядами, оставляющими за собой дымный след.
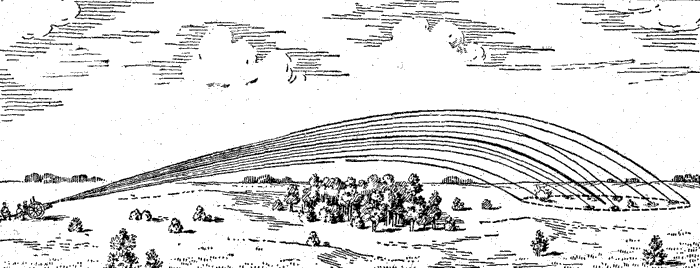 |
| Рис. 198. Пучок траекторий снарядов |
Разбрасывания снарядов - их рассеивания - избежать невозможно.
Значит, попадание третьим снарядом, как это удалось нашим артиллеристам, является несомненно достижением, и такая стрельба может быть названа точной.
Но если рассеивание снарядов неизбежно, это совсем не означает, что на него надо махнуть рукой. Отнюдь нет.
Все, что в наших силах, мы должны сделать.
Мы должны, во-первых, до предела уменьшить рассеивание снарядов. Чем и как этого достигают, вы уже знаете из только что рассказанного.
Мы должны, во-вторых, как-то приспосабливаться к рассеиванию снарядов, учитывать его заранее, чтобы оно не заставало нас каждый раз врасплох, не путало все наши расчеты и не причиняло нам непоправимого вреда.
Мы должны, в-третьих, выбирать на поле боя цель для стрельбы в соответствии с известным нам рассеиванием снарядов. Иначе, как мы скоро увидим, может получиться "стрельба из пушки по воробьям".
Очевидно, для того чтобы справиться с этими задачами, нам надо найти и изучить закон рассеивания снарядов.
Невозможно предсказать точно, куда упадет выпущенный из орудия снаряд: тут в ваши расчеты вмешивается случайность.
Зато, если вы выпустите из орудия, не изменяя наводки, много снарядов, произведете по цели, скажем, сотню выстрелов или больше, то тут вы уже сможете предсказать, как упадут снаряды.
Результаты случайных явлений, оказывается, тоже подчиняются некоторой количественной закономерности. Рассеивание снарядов только на первый взгляд происходит совершенно беспорядочно. На самом же деле результаты рассеивания подчиняются определенному закону.
Итак, предположим, что вы действительно произвели из орудия подряд сто выстрелов. Ваши снаряды упали где-то на расстоянии нескольких километров от орудия, разорвались и вырыли в земле сто воронок.
Как расположатся эти воронки?
Прежде всего, участок, в котором заключаются воронки, образует некоторую геометрическую фигуру. Если вы очертите этот участок по всем крайним воронкам, то получите вытянутую в направлении стрельбы фигуру, похожую на эллипс (рис. 199). За границами этого эллипса воронок совсем не будет.
Но этого мало. Внутри эллипса воронки распределятся по некоторому, очень простому, правилу: чем ближе к центру эллипса, тем гуще, ближе одна от другой будут лежать воронки; чем дальше от центра, тем они будут лежать реже, а у самых краев эллипса их будет совсем мало.
Таким образом, в пределах площади рассеивания всегда будет такая точка, около которой окажется наибольшее число попаданий; точка эта совпадет с центром эллипса. Эта точка, около которой можно с наибольшей вероятностью ожидать падения снарядов, называется средней точкой падения (рис. 199). Ей соответствует средняя траектория снарядов, то-есть траектория, проходящая в середине снопа.
Если бы никакие случайности не вмешивались в стрельбу, то все снаряды полетели бы один за другим как раз по этой средней траектории и попали бы в самый центр эллипса.
Относительно средней точки падения все воронки будут группироваться, до известной степени, симметрично.
Если стать в том месте площади рассеивания, где наиболее густо расположились воронки, - в средней точке падения, - то можно заметить, что впереди этой точки упало снарядов примерно столько же, сколько и позади, а вправо примерно столько же, сколько и влево (рис. 199).
Таков закон рассеивания снарядов при стрельбе.
Без знания этого закона нельзя считать себя грамотным стрелком-артиллеристом .
Знание этого закона приносит артиллеристу большую пользу: оно подсказывает, сколько нужно выпустить снарядов по цели, чтобы рассчитывать на попадание.
Но чтобы извлечь из этого закона всю пользу, которая в нем таится, нужно его прежде всего сформулировать математически.
Сделать это совсем не трудно.
Для этого прежде всего проведите ось рассеивания по дальности (на рис. 199 линия АБ). Этой осью явится такая линия, перед которой и за которой число воронок будет одинаковым, то-есть по 50.
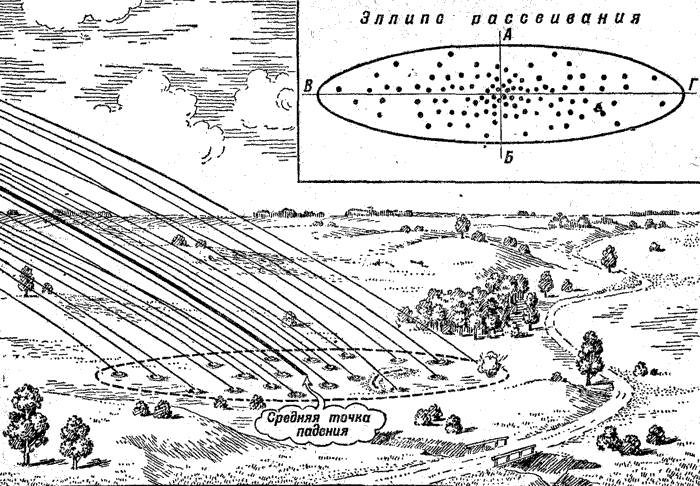 |
| Рис. 199. Рассеивание снарядов; справа вверху - примерное распределение сотни воронок |
Теперь отсчитайте 25 воронок, расположенных ближе других к оси рассеивания по одну ее сторону, и отделите эти воронки линией, параллельной оси рассеивания (рис.200). Ширина полученной вами полосы - очень важный показатель рассеивания; ее называют "срединным отклонением" по дальности. Действительно, если вы отложите такую же полосу по другую сторону оси рассеивания, то в двух этих полосах у вас будет заключена "лучшая" половина всех попаданий. Лучшая потому, что эти 50 попаданий легли густо около средней точки падения.
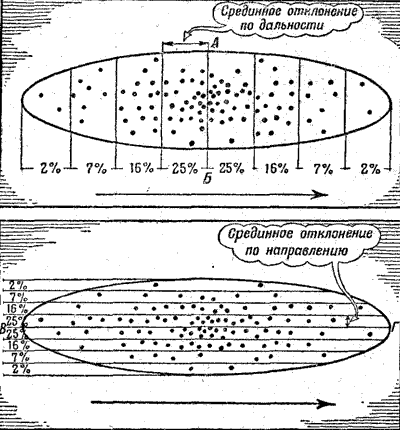 |
| Рис. 200. Процентное распределение сотни воронок в эллипсе рассеивания |
Если теперь вы будете дальше откладывать вперед и назад полосы, равные срединному отклонению, то можно будет установить математическое выражение закона рассеивания. Вы увидите, что таких полос получится у вас всего 8, по 4 в каждую сторону от оси рассеивания (рис. 200). И в каждой полосе окажется определенное число воронок, показанное на рисунке.
То же самое получится и в том случае, если вы проведете полосы не поперек, а вдоль эллипса (рис. 200).
25%, 16%, 7%, 2% - эти числа стоит запомнить, они вам пригодятся: ведь это и есть численное выражение закона рассеивания.
Из какого бы орудия вы ни стреляли, все равно попадания снарядов распределятся по этому закону.
Конечно, если вы произведете немного выстрелов, то вы получите, может быть, не совсем такие числа. Но чем больше выстрелов произведено, тем яснее будет проявляться закон рассеивания.
Закон этот действителен во всех случаях: стреляете ли вы по малой цели или по большой, далеко или близко, из такого орудия, которое очень сильно рассеивает снаряды, или из такого, которое рассеивает снаряды мало,-обладает, как говорят артиллеристы, большой "кучностью боя". Вся разница будет в том, что в одном случае у вас получится большой эллипс, а в другом - малый.
Чем больше эллипс, чем шире каждая из его восьми полос, тем, значит, рассеивание больше. Наоборот, чем эллипс меньше, чем каждая из его восьми полос уже, тем, значит, рассеивание меньше.
По срединному отклонению вы можете, таким образом, судить о величине рассеивания, о кучности боя орудия.
Из рисунков ясно видно, что срединное отклонение боковое всегда меньше, чем срединное отклонение по дальности. Это значит: всякое орудие больше рассеивает снаряды по дальности (вперед-назад), чем в стороны (вправо-влево).
Мы уже знаем, что траектории снарядов, если смотреть на них от орудия, имеют вид расходящегося снопа (рис. 198).
Ясно, что траектории разойдутся тем больше, - а в связи с этим и рассеивание будет тем больше, - чем на большую дальность мы стреляем.
Примерные размеры эллипсов рассеивания для двух наших орудий при стрельбе на разные дальности показаны на рисунке 201.
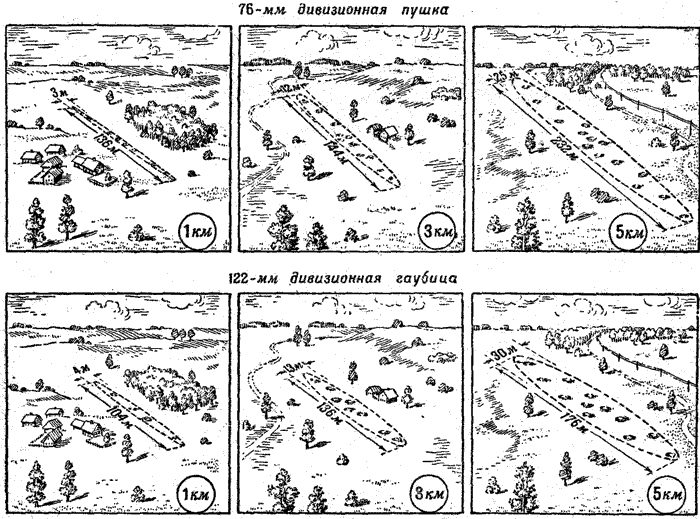 |
| Рис. 201. Чем больше дальность стрельбы, тем больше и рассеивание. У гаубицы рассеивание снарядов по дальности меньше, чем у пушки |
В бою всегда приходится помнить о рассеивании и считаться с ним.
Именно поэтому, прежде чем начать стрельбу по какой-нибудь цели, артиллерист должен продумать, сколько приблизительно понадобится снарядов, чтобы эту цель поразить, есть ли вообще смысл тратить на эту цель такое количество снарядов.
Цель маловажная - да еще малых размеров - не должна соблазнять артиллериста. Стрельба по такой цели приводит только к лишнему расходу снарядов и времени. А в бою очень дороги каждый снаряд и каждая минута.
Стрелять из артиллерийского орудия в боевой обстановке - это совсем не то, что стрелять из ружья в садовом тире, где много занимательных фигур - целей. В тире вы можете стрелять по любой цели. В бою же от артиллериста требуется не только умение стрелять, но еще и умение правильно выбирать цель.
Вот, например, какой-то всадник противника показался на дороге, удаленной на 5 километров от нашей дивизионной пушки. В бинокль его отлично видно на фоне неба. Вот он остановился, как будто изучает поле боя. Быть может, это .крупный вражеский начальник? Имеет ли, однако, смысл открыть по этой цели огонь из пушки? Посмотрите на рисунок 201. На дальность в 5 километров наша пушка дает эллипс рассеивания длиной 232 метра и шириной 25 метров. Можно ли при этих условиях рассчитывать на попадание в отдельного всадника не только целым снарядом, но даже отдельным осколком или шрапнельной пулей? Очевидно, для этого понадобились бы очень много снарядов, и то без всякой уверенности в успехе стрельбы. А так как цель эта в данный момент ничем особо не вредит нашим войскам, стрельба по ней явно не имеет смысла - это была бы действительно "стрельба из пушки по воробьям".
Бессмысленность стрельбы по мелким, неважным удаленным целям - не единственный результат рассеивания. Бывают случаи, когда рассеивание причиняет крупные неприятности.
Вот, например, случай, когда наша и неприятельская пехота приходят в близкое соприкосновение друг с другом: тут уж рассеивание может послужить даже причиной "стрельбы по своим".
Когда цель находится недалеко от нашей пехоты, некоторые снаряды вследствие рассеивания могут не долететь до цели, упасть ближе, чем нужно, в наше расположение. Так, например, если наша артиллерия ведет стрельбу через нашу пехоту, примерно на 3-4 километра, то находиться ближе 200-250 метров от цели уже опасно. В этом случае наша пехота может быть поражена не только осколками (от них еще можно укрыться), но и целыми снарядами. Поэтому, как только наша пехота подойдет к цели ближе чем на 250 метров, артиллерия, стрелявшая через пехоту, сейчас же переносит огонь несколько дальше и предоставляет пехоте бороться с ближними целями своими средствами.
Поэтому-то, между прочим, пехота и имеет свою собственную артиллерию, которая передвигается вместе с пехотой и в такие моменты поражает важные ближние цели своим метким огнем.
Если же артиллерия стреляет не фронтальным, а фланговым огнем, то-есть с позиции, находящейся сбоку (рис. 202), то своя пехота может подойти к цели значительно ближе: в этом случае опасным является рассеивание снарядов только в стороны, а оно, как мы знаем, всегда значительно меньше, чем рассеивание в направлении стрельбы.
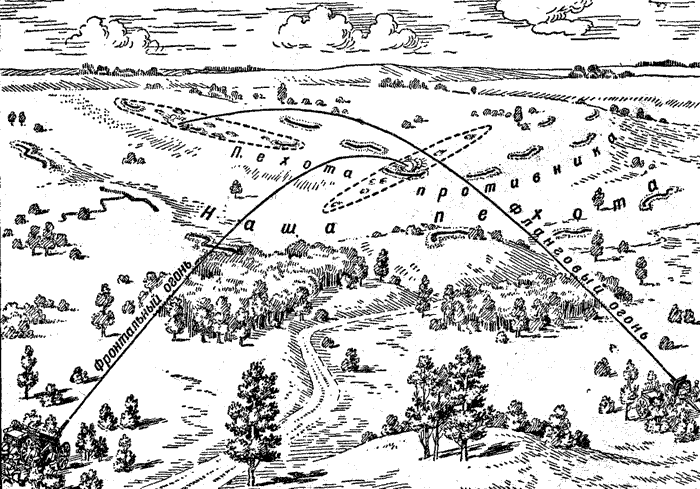 |
| Рис. 202. Фланговый огонь по пехоте противника, расположенной вдоль фронта, выгоднее фронтального огня. Пунктиром обведены площади рассеивания снарядов; видны воронки |
По той же причине, как видно из рисунка 202, фланговый огонь артиллерии наносит гораздо большее поражение вытянутым вдоль фронта войскам (окопам) противника, чем огонь фронтальный.
Кроме рассеивания по дальности и рассеивания по направлению имеется еще рассеивание по высоте. Иначе и не может быть: ведь снаряды летят не по одной и той же траектории, а расходящимся снопом.
Если бы мы поставили на пути летящих снарядов большой деревянный щит так, чтобы каждый летящий снаряд пробил в нем отверстие, то мы увидели бы, как происходит рассеивание по высоте (рис. 203).
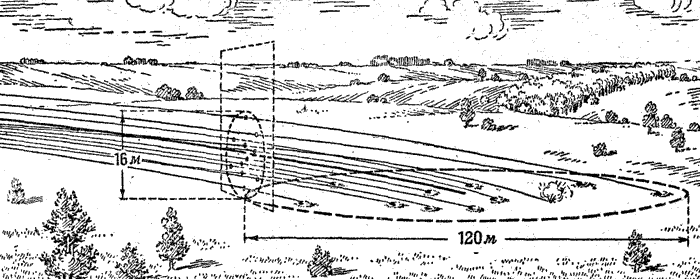 |
| Рис. 203. Рассеивание траекторий по высоте |
Вертикальная площадь рассеивания и по размерам, и по форме будет иная, чем площадь рассеивания на горизонте. Рассеивание по высоте обычно будет гораздо меньшим, чем рассеивание по дальности, и все более и более резко будет отличаться от него по мере приближения цели к орудию.
Например, при стрельбе гранатой из 76-миллиметровой дивизионной пушки на дальность 1 600 метров рассеивание по высоте равно лишь 16 метрам, а рассеивание по дальности в этом же случае равно примерно 120 метрам (рис. 203).
Небольшое рассеивание по высоте позволяет легко поражать такие цели, которые выдаются над поверхностью земли и находятся при этом сравнительно недалеко от орудия. В таких условиях, например, происходит часто стрельба по танкам.
Здесь меньше всего сказывается вредное влияние рассеивания.
Понятия "рассеивание" и "кучность" противоположны друг другу.
Чтобы быстрее поражать цели, нужно прежде всего добиться от орудия наибольшей возможной для него кучности боя, то-есть наименьшего рассеивания снарядов.
А для этого, как мы говорили уже, нужно очень бережно обращаться с орудием, очень тщательно и однообразно наводить его, подбирать по весу снаряды, тщательно заряжать и так далее. Только при этих условиях снаряды упадут кучно, ближе один к другому, и вы получите менее расходящийся сноп траекторий.
 |
| Рис. 204. Средняя траектория - перед целью |
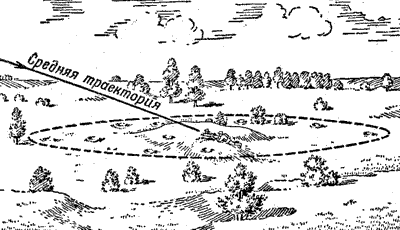 |
| Рис. 205. Средняя траектория проходит через цель |
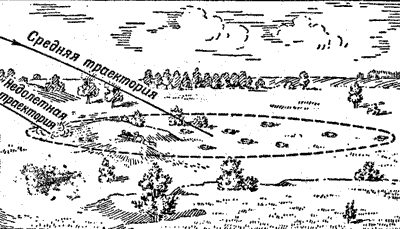 |
| Рис. 206. Хотя средняя траектория - перелетная, снаряд все же не долетел до цели - это результат рассеивания траекторий |
Но всего этого еще мало для успешного поражения цели: орудие может посылать снаряды очень кучно, и все же большая часть этих снарядов, а, быть может, даже все, не попадут в цель. Так получится, если вы не метко стреляете, то-есть взяли неправильный прицел или ошиблись в направлении. Иными словами, так получится в том случае, когда средняя точка падения (центр эллипса рассеивания) не совпадет с целью (рис. 204).
Метким артиллеристом мы называем такого стрелка, который умеет свои снаряды (сноп траекторий) направить так, чтобы средняя траектория проходила через цель (рис. 205). Только в этом случае можно ожидать быстрого поражения цели, так как цель окажется как раз в той части эллипса рассеивания, где снаряды упадут наиболее густо.
Тут может возникнуть вопрос: как же во время стрельбы узнать, что средняя траектория прошла через цель или близко от нее? Ведь это какая-то воображаемая траектория в середине снопа. По каким же признакам можно догадаться, где прошла эта средняя траектория?
При отсутствии рассеивания вопрос этот решился бы совсем просто. Если бы вы получили при первом выстреле разрыв перед целью, то-есть недолет, вы знали бы наверняка, что недолет этот не случайный, а вызванный ошибкой в ваших расчетах. Вы измерили бы расстояние от первого разрыва до цели и соответственно этому расстоянию увеличили бы установку прицела на нужное число делений. Тогда, наверное, траектория прошла бы совсем близко от цели и даже, может быть, через цель. Так просто поступили бы вы, если бы не существовало рассеивания.
Но рассеивание и тут сильно осложняет дело.
Если первый разрыв оказался недолетным, то это еще вовсе не значит, что прицел взят неправильно и средняя траектория снарядов недолетная. Недолет мог быть случайным: недолеты имеют место и тог да, когда установка прицела взята правильно и средняя траектория проходит как раз через цель; недолет может случиться даже и при перелетной средней траектории.
На рисунке 206 показан как раз такой случайный недолет, когда средняя траектория-перелетная, то-есть проходит за целью.
Вы видите, что в этом случае, при недолете, нужно было бы не прибавлять, а, наоборот, убавлять прицел, чтобы подвести среднюю траекторию к цели.
Таким образом, по одному недолету или перелету еще нельзя с уверенностью решить, где именно проходит средняя траектория, какой прицел будет правильным. Это можно решить только тогда, когда будет выпущено несколько снарядов.
Действительно, если бы при том положении траектории, как она показана на рисунке 206, было сделано несколько выстрелов, то что мы могли бы наблюдать?
Мы увидели бы, что большая часть разрывов оказалась за целью и только меньшая часть - перед целью. Это получилось бы потому, что на основании закона рассеивания большая часть разрывов сгруппировалась бы поблизости от средней точки падения, - а она во взятом примере перелетная.
Отсюда можно вывести правило: получение при одной установке прицела большего числа перелетов, нежели недолетов, служит признаком перелетной средней траектории. И наоборот - при недолетной средней траектории недолетов будет получаться больше, чем перелетов (рис. 207).
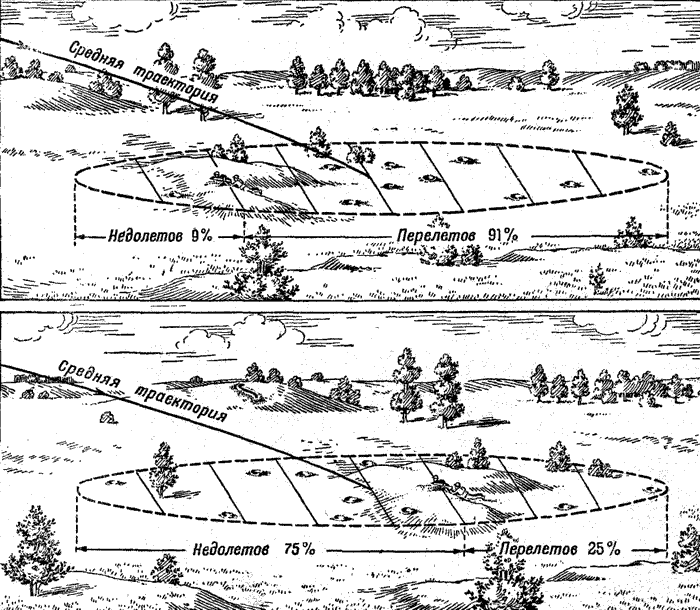 |
| Рис. 207. Процентное распределение перелетов и недолетов, когда средняя траектория проходит за целью на два срединных отклонения, и когда средняя траектория недолетная на одно срединное отклонение (для наглядности цель показана не в масштабе рисунка, а значительно крупнее) |
Ну, а если средняя траектория проходит как раз через цель? Тогда разрывы распределятся численно симметрично относительно средней точки падения (цели), они дадут приблизительно равное число как недолетов, так и перелетов. Это и будет признаком того, что стрельба ведется правильно (рис. 208).
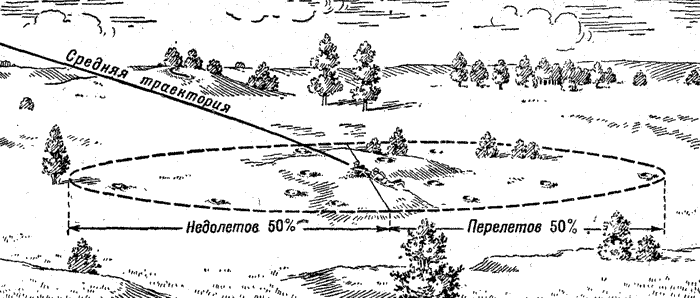 |
| Рис. 208. При стрельбе гранатой равенство недолетов и перелетов указывает, что средняя траектория проходит как раз через цель |
Чтобы добиться этого, приходится обычно не один раз изменять установки прицела и испытывать их несколькими выстрелами. Чтобы быстрее решить эту задачу, артиллеристы пользуются специально разработанными правилами.
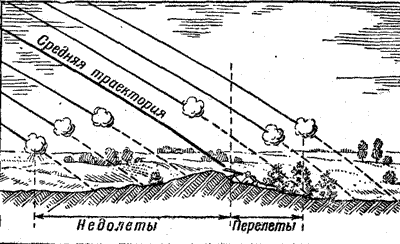 |
| Рис. 209. Если при стрельбе шрапнелью (разрывы в воздухе) средняя траектория проходит через цель, то недолетов будет больше, чем перелетов |
Нужно, однако, сказать, что равенство недолетов и перелетов характеризует правильную стрельбу только в том случае, если разрывы происходят на земле, то-есть если огонь ведется гранатой. Когда же разрывы происходят в воздухе, - а это бывает при стрельбе шрапнелью, - выгоднее, чтобы недолетов было больше, чем перелетов.
На рисунке 209 показан сноп траекторий шрапнелей и средняя их траектория, проходящая через цель. Разрывы происходят в воздухе. Пунктирная линия, проведенная вертикально над целью, отделяет недолетные разрывы от перелетных. Недолетных разрывов, как видно, больше, чем перелетных, хотя прицел взят правильно.
Итак, знание закона рассеивания помогает решать основной вопрос, как надо стрелять, чтобы поразить цель быстро, при наименьшем расходе снарядов.
Артиллериста всегда интересует еще и такой вопрос: какая часть выпущенных им снарядов попадет, по всей вероятности, в цель, а какая может пролететь мимо? Иначе говоря: с какой вероятностью можно ожидать попадания в цель?
Ответ на этот вопрос дает все тот же закон рассеивания снарядов.
Вероятность попадания выражают обычно в процентах. Так, например, если говорят: вероятность попасть в цель-20%, то это означает, что на каждые сто выпущенных снарядов можно ждать двадцать попаданий, остальные же восемьдесят снарядов, вероятно, дадут промах.
Для определения вероятности попадания приходится учитывать:
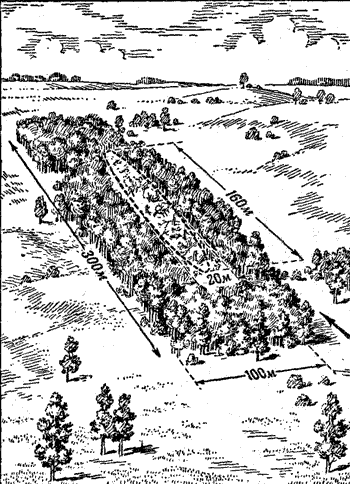
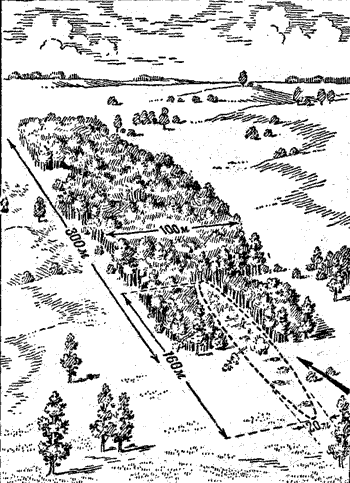
Допустим, что нужно обстрелять рощу, в которой укрываются танки и пехота противника. Роща занимает в глубину 300 метров и в ширину 100 метров (рис. 210). 76-миллиметровая дивизионная пушка стреляет гранатой. Дальность стрельбы-4 000 метров. На эту дальность площадь рассеивания в глубину будет около 160 метров, а по ширине-20 метров. Таким образом, площадь рассеивания меньше площади цели. Значит, если прицел взят правильно и средняя траектория пройдет через середину рощи, то сколько бы ни было выпущено снарядов, все они непременно попадут в рощу. В этом случае можно сказать: вероятность попадания в рощу равна 100%.
 |
 |
|
| Рис. 210. Площадь рассеивания меньше площади рощи и средняя траектория проходит через центр рощи - все снаряды попадут в цель | Рис. 211. Площадь рассеивания меньше площади рощи, но средняя траектория проходит через край рощи - в цель попадет 50% снарядов |
Нужно ли быть метким стрелком, чтобы попасть в такую большую цель?
Конечно, нужно. Ведь если стреляющий возьмет не совсем верный прицел и направит среднюю траекторию не в центр рощи, а скажем, в ее передний край, то половина всех снарядов не попадет в цель, не долетит до рощи. Вероятность попадания будет тогда всего 50% (рис. 211).
Возьмем теперь цель, размеры которой меньше площади рассеивания, и рассчитаем опять-таки вероятность попадания. Мы увидим, что для поражения такой цели большое значение будет иметь не только совпадение средней траектории с серединой цели, но еще и кучность боя орудия.
Требуется, например, сделать проход в проволочном заграждении, причем глубина этого заграждения 20 метров. Положим, что стреляет 122-миллиметровая гаубица на 3 200 метров; при этом срединное отклонение по дальности равно 20 метрам.
Спрашивается: какова вероятность попадания в проволочное заграждение, если средняя траектория проходит через его передний край? .
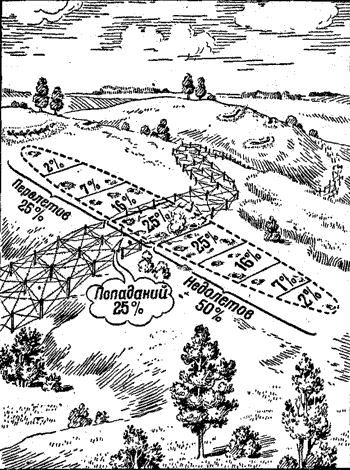
На рисунке 212 показано положение площади рассеивания и цели. Площадь рассеивания разделена на полосы (срединные отклонения), в каждой полосе проставлена вероятность попадания в процентах.
 |
 |
|
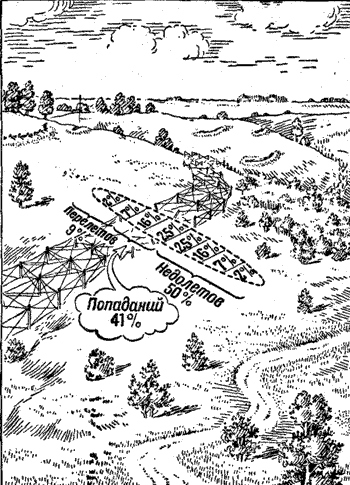
| Рис. 212. "Средняя траектория проходит через передний край проволочного заграждения. При дальности стрельбы 3 200 метров вероятность попадания 25% | Рис. 213. Средняя траектория проходит через передний край проволочного заграждения. При дальности стрельбы 1 600 метров вероятность попадания 41% |
Рассматривая рисунок, вы видите, что цель накрывается одной полосой, содержащей 25% попаданий.
Таким образом, можно ожидать, что из 100 выпущенных снарядов в проволоку попадет 25, а остальные пролетят мимо, то-есть вероятность попадания-25% и вероятность промаха-75%.
Если дальность до цели будет не 3 200 метров, а меньше, например 1600 метров, то при стрельбе из того же орудия рассеивание будет меньше и вероятность попадания возрастет. Положение площади рассеивания и цели для этого случая показано на рисунке 213, где срединное отклонение по дальности взято равным 10 метрам. Проволочное заграждение глубиной в 20 метров покрывается уже не одной, а двумя полосами - с 25% и с 16% попаданий. Вероятность попадания в этих условиях составляет 25% + 16% = 41%.
Таким образом, с уменьшением дальности стрельбы вероятность попадания становится больше, так как увеличивается кучность боя. Вероятность попадания была 25%, а стала 41%.
Попробуйте рассчитать сами вероятность попадания в такое же проволочное заграждение на дальности 1 600 метров, но в условиях более меткой стрельбы, когда средняя траектория проходит как раз через середину цели. Вы увидите, что вероятность попадания еще возрастет. Она будет равна 50%.
Сделать подсчет вероятности попадания всегда полезно, особенно при стрельбе на большие дальности и по небольшим целям; такая стрельба сопряжена со значительным расходом снарядов.
Представим себе, например, что 122-миллиметровая гаубица стреляет по блиндажу, который находится на расстоянии 5 километров от нее. Какова вероятность попадания в этот блиндаж, если он имеет размеры всего около 20-25 квадратных метров?
И расчеты показывают, и практика подтверждает, что в этих условиях вероятность попадания будет около 2%. Таким образом, при стрельбе по такой небольшой цели, как блиндаж, может потребоваться для его разрушения более сотни снарядов.
И при этом расходе снарядов можно рассчитывать в среднем только на 2-3 попадания.
Успех подобной стрельбы зависит не только от стреляющего командира, то-есть от его умения вести стрельбу, но и в большой степени от наводчика, выполняющего команды во время стрельбы. От наводчика всегда требуется возможно большая точность наводки при каждом выстреле.